Question

please explain your steps and answers write clearly so i can follow 1) The dynamics of an inverted pendulum are given as \( \quad m L \ddot{\theta}+m g l \sin (\theta)=\tau(t) \) where \( \mathrm{m} \) is the mass of the pendulum, \( \mathrm{L} \) is the length of the

Answer 1

The equation of motion for the inverted pendulum is
`\( m L \ddot{\theta} + m g l \sin(\theta) = \tau(t) \).`

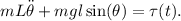
Step-by-step explanation:

The given equation describes the dynamics of an inverted pendulum, where ( m ) is the mass of the pendulum, ( L ) is the length,
`\ddot{\theta} \)` is the angular acceleration, ( g ) is the acceleration due to gravity, ( l ) is the distance from the pivot point to the center of mass, and
`\( \tau(t) \)` is the external torque applied.

The term
`\( m L \ddot{\theta} \)` represents the inertia of the pendulum, and
`\( m g l \sin(\theta) \)` accounts for the gravitational torque. The equation essentially states that the sum of the inertial torque and gravitational torque equals the external torque applied
`(\( \tau(t) \))`.

This second-order differential equation is nonlinear due to the presence of the sine term. Solving such equations requires advanced mathematical techniques, often involving numerical methods or analytical approximations. The solution would yield the function
`\( \theta(t) \),` describing the angular position of the pendulum over time in response to the applied torque.

Understanding and analyzing the dynamics of an inverted pendulum are crucial in control systems, robotics, and various engineering applications. The equation provides insights into how external forces influence the motion of the pendulum, and solving it helps in designing control strategies to stabilize or manipulate the system for desired outcomes.