Question

Consider a production function of the following form: Q(KL)=5K/12 a) What would you call this particular type of functional form? b) Is there any assumption which you would usually make regarding K and L, and why is this economically sensible? c) Setequal to 10 and rearrange the function so that it is in the form K = S(L). What does this function represent? d) Using your answer from e) find an expression for the marginal rate of substitution (MRS) between K and L, and explicitly state, given the assumptions you made in

Answer 1

a) The given production function,
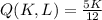`\(Q(K,L) = (5K)/(12)\)`, represents a Cobb-Douglas functional form.

b) The Cobb-Douglas functional form assumes constant returns to scale, implying that the exponents on capital
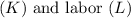`(\(K\)) and labor (\(L\))` sum to 1. This assumption is economically sensible as it allows for flexibility in adjusting inputs while maintaining a consistent output scale.

c) Setting
`\(Q = 10\) and rearranging the function, we get \(K = (24)/(5)L\)`.

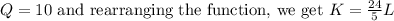Explanation:

a) The Cobb-Douglas functional form is characterized by a production function of the form
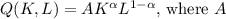`\(Q(K, L) = A K^(\alpha) L^(1-\alpha)\), where \(A\)` is a positive constant and
`\(\alpha\)` is the output elasticity of capital. In the given production function
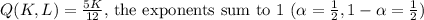`\(Q(K, L) = (5K)/(12)\), the exponents sum to 1 (\(\alpha = (1)/(2), 1-\alpha = (1)/(2)\))`, confirming it as a Cobb-Douglas form.

b) The assumption of constant returns to scale is integral to the Cobb-Douglas model. It means that if both inputs, capital
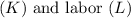`(\(K\)) and labor (\(L\))`, are increased by a certain factor, output
`(\(Q\))` will increase by the same factor. This assumption aligns with economic intuition, as it allows for easy interpretation of the impact of input changes on output.

c) Setting
`\(Q = 10\) and rearranging the given function \(Q(K, L) = (5K)/(12)\) results in \(K = (24)/(5)L\)`. This expression represents a linear relationship between capital
`(\(K\)) and labor (\(L\)) with a slope of \((24)/(5)\)`.

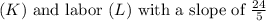In conclusion, the Cobb-Douglas functional form provides a useful framework for analyzing production relationships, and the constant returns to scale assumption simplifies the interpretation of input-output dynamics in economic production models. The rearranged function
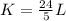`\(K = (24)/(5)L\)` expresses the proportional relationship between capital and labor in the given production context.