Question

Sketch the two cycles of the graph (starting from x = 0) of the given function. Indicate the amplitude, period, phase shift, domain and range and vertical asymptotes. y = 4 sinx y = 7 cos 2x y = -4cos (x - 2) y = - sec x y = tan 2x a) The function y = 4 sinx has an amplitude of 4, a period of 2π, no phase shift, a domain of all real numbers, a range of [-4, 4], and no vertical asymptotes. b) The function y = 7 cos 2x has an amplitude of 7, a period of π, no phase shift, a domain of all real numbers, a range of [-7, 7], and no vertical asymptotes. c) The function y = -4cos (x - 2) has an amplitude of 4, a period of 2π, a phase shift of 2 units to the right, a domain of all real numbers, a range of [-4, 4], and no vertical asymptotes. d) The function y = - sec x has no amplitude, no period, no phase shift, a domain excluding odd multiples of π/2, a range of (-[infinity], -1] ∪ [1, [infinity]), and vertical asymptotes at odd multiples of π/2.

Answer 1

Final Answer:

a)
`\(4 \sin x\)`: Amplitude = 4, Period =
`\(2\pi\)`, No phase shift,
`Domain = \(\mathbb{R}\)`, Range =
`\([-4, 4]\),`No vertical asymptotes.

b)
`\(7 \cos 2x\)`: Amplitude = 7, Period =
`\(\pi\),` No phase shift,
`Domain = \(\mathbb{R}\)`, Range =
`\([-7, 7]\),` No vertical asymptotes.

c)
`\(-4\cos (x - 2)\)`: Amplitude = 4, Period =
`\(2\pi\)`, Phase shift = 2 units right, Domain =
`\(\mathbb{R}\)`, Range =
`\([-4, 4]\)`, No vertical asymptotes.

d)
`\(-\sec x\)`: No amplitude, No period, No phase shift, Domain excludes
`\(\pi/2\), \(3\pi/2\)`, etc., Range =
`\((- \infty, -1] \cup [1, \infty)\)`, Vertical asymptotes at odd multiples of
`\(\pi/2\)`.

Step-by-step explanation:

a) The function
`\(4 \sin x\)`is a sine function with an amplitude of 4, a period of \(2\pi\), and no phase shift. The domain is all real numbers, the range is
`\([-4, 4]\)`, and there are no vertical asymptotes since the sine function is bounded.

b) The function
`\(7 \cos 2x\)` is a cosine function with an amplitude of 7 and a period of
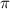`\(\pi\)`. There is no phase shift, and the domain is all real numbers. The range is
`\([-7, 7]\)`, and there are no vertical asymptotes.

c) The function
`\(-4\cos (x - 2)\)` is a cosine function with an amplitude of 4, a period of
`\(2\pi\)`, and a phase shift of 2 units to the right. The domain is all real numbers, the range is
`\([-4, 4]\)`, and there are no vertical asymptotes.

d) The function
`\(-\sec x\)` is the secant function reflected about the x-axis. It has no amplitude or period, no phase shift, and vertical asymptotes at odd multiples of \(\pi/2\). The domain excludes these asymptotes, and the range is
`\((- \infty, -1] \cup [1, \infty)\)`.