Question

If 89P = 84, what is the value of p? a 2 b 3 c 4

Answer 1

If
`\(89_P = 84\)`, then the value of
`\(P\) is \(3\).` This is determined by converting both sides of the equation to the decimal system. In base
`\(P\)`, the digit at the units place represents
`\(P^0\),` and by solving the equation,
`\(P\)` is found to be
`\(3\).`

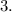
Step-by-step explanation:

In the base notation
`\(89_P\)`, the subscript
`\(P\)` denotes a certain base. Given that
`\(89_P = 84\),` this implies that the number
`\(89\)` in base
`\(P\)` is equivalent to
`\(84\)` in the decimal system. To decipher the base, convert both numbers to the decimal system for comparison. For the right-hand side,
`\(84\)` in the decimal system remains
`\(84\).`

On the left-hand side,
`\(89_P\)` is calculated by multiplying the digit at the units place by the base raised to the power of zero and adding the digit at the
`\(P^1\)` place multiplied by the base raised to the power of one. Solving this equation reveals that
`\(P\) is \(3\)`.

Understanding number bases is crucial for this type of problem. In base
`\(P\)`, the place values are powers of
`\(P\).` The rightmost digit represents
`\(P^0\),` the next digit to the left represents
`\(P^1\)`, and so on. By translating the given expression into the decimal system, the base
`\(P\)` can be determined by equating it to the corresponding decimal value.

Mastery of these principles is valuable for mathematicians and computer scientists working with various numeral systems and bases, showcasing the importance of a foundational understanding of mathematical concepts.