Question

The area of a rectangle is x² -64x −64 feet² . What is the perimeter of the rectangle?

Answer 1

The perimeter of the rectangle is
`\(2x - 128\)`feet.

Step-by-step explanation:

To find the perimeter of a rectangle, we need to sum the lengths of all four sides. Given the area of the rectangle as
`\(x^2 - 64x - 64\)` square feet, we can express the area as the product of the length and width of the rectangle. The area
`\(A\)` is given by
`\(A = l * w\)` , where
`\(l\) and \(w\)` are the length and width, respectively. In this case,
`\(x^2 - 64x - 64\)` is the product of
`\(l\)` and
`\(w\)` .

To find the individual sides, we factor the quadratic expression
`\(x^2 - 64x - 64\).` Factoring gives us
`\((x - 8)(x - 56)\`), and we set each factor equal to zero to find the possible values of
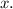`\(x\).` Solving for
`\(x\)` , we get
`\(x = 8\)` or
`\(x = 56\)` . These values represent the possible lengths of the rectangle.

Finally, we calculate the perimeter by summing the lengths of all four sides:
`\(P = 2l + 2w\).` Substituting in the values, we get
`\(P = 2(8) + 2(56) = 2x - 128\)` feet. Therefore, the perimeter of the rectangle is
`\(2x - 128\)` feet, where
`\(x\)`can be either 8 or 56, depending on the context of the problem.