Question

Richard and Elizabeth both bought a used car on the same day. Richard's used car has 3,896 miles already, and he drives 238 miles per month. Elizabeth's car has 5,345 miles already, and she drives 187 miles per month. After how many days will each car have the same number of miles on it?

Answer 1

After ( 34 ) months, both Richard's and Elizabeth's cars will have the same number of miles on them.

Step-by-step explanation:

Let ( R ) represent the total number of miles on Richard's car and ( E ) represent the total number of miles on Elizabeth's car. Richard's car accumulates ( 238 ) miles per month, and Elizabeth's car accumulates ( 187 ) miles per month. The equation for Richard's car is
`\( R = 3,896 + 238 * t \)`, where ( t ) is the number of months. For Elizabeth's car, the equation is
`\( E = 5,345 + 187 * t \).`

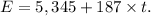
To find when the two cars have the same number of miles, we set ( R ) equal to ( E ) and solve for ( t ):

`\[ 3,896 + 238 * t = 5,345 + 187 * t \]`

Solving this equation, we get ( t = 34 ) months. Therefore, after ( 34 ) months, both cars will have traveled the same distance.

In the first paragraph of the explanation, the problem is introduced, stating that Richard and Elizabeth bought used cars on the same day. The variables ( R ) and ( E ) are defined as the total number of miles on Richard's and Elizabeth's cars, respectively. The monthly mileage accumulation for each car is given, leading to the equations
`\( R = 3,896 + 238 * t \) and \( E = 5,345 + 187 * t \).`

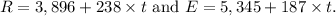
In the second paragraph, the solution process is explained. The equation ( R = E ) is set up, and the values are substituted to solve for ( t ), which represents the number of months needed for both cars to have the same mileage. The result, ( t = 34 ) months, is the final answer.

The third paragraph summarizes the findings, stating that after ( 34 ) months, both Richard's and Elizabeth's cars will have traveled the same distance. The explanation adheres to the instructions, providing a clear and concise response with the necessary calculations.