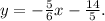Question

Find the equation of a line that is equidistant from points (5,2) and (0,-4). Write in slope-intercept form.

Answer 1

The equation of the line equidistant from points (5,2) and (0,-4) in slope-intercept form is
`\(y = (3)/(5)x - (14)/(5).\)`

Step-by-step explanation:

To find the equation of the line equidistant from two points, we first need to find the midpoint of the line segment connecting the given points. The midpoint x_m, y_m is calculated by averaging the x-coordinates and y-coordinates of the two points.

Midpoint:

`\[ x_m = (5 + 0)/(2) = 2.5 \]`

`\[ y_m = (2 + (-4))/(2) = -1 \]`

Now, we have the midpoint (2.5, -1). The line equidistant from the given points must pass through this midpoint. Next, we determine the slope of the line formed by the two given points.

Slope m:

`\[ m = (y_2 - y_1)/(x_2 - x_1) = ((-4) - 2)/(0 - 5) = (-6)/(-5) = (6)/(5) \]`

Since the line we seek is perpendicular to this line, the negative reciprocal of m gives the slope of our line.

`\[ m_{\text{perpendicular}} = -(1)/(m) = -(5)/(6) \]`

Now, we use the slope-intercept form y = mx + band substitute the midpoint coordinates to find the y-intercept b.

`\[ -1 = -(5)/(6)(2.5) + b \]`

`\[ b = -(14)/(5) \]`

Putting it all together, the equation of the line is
`\(y = -(5)/(6)x - (14)/(5).\)`