Question

A pitcher throws a 0.14-kg baseball with a speed of 28.8 m/s. The batter strikes it with an average force of 5000 N, which results in the ball traveling with an initial speed of 37.0 m/s toward the pitcher. For how long we’re the bat and ball in contact?

Answer 1

Given data:

* The velocity of the ball before hitting is,

`u=28.8\text{ m/s}`

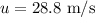
* The velocity of the ball after hitting the bat is,

`v=-37\text{ m/s}`

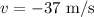
Here, the negative sign is indicating the direction of motion of ball is in opposite direction to the direction of motion before hitting by the bat.

* The mass of the ball is,

`m=0.14\text{ kg}`

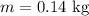
* The average force on the ball by the bat is,

`F=5000\text{ N}`

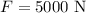
Solution:

The change in the momentum of the ball after hitting is,

`\Delta p=p_2-p_1`

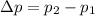
where p2 is the momentum of the ball after hitting from the bat and p1 is the momentum of the ball before hitting from the bat,

The change in momentum in terms of mass is,

`\begin{gathered} \Delta p=mv-m\text{u} \\ =m\mleft(v-u\mright) \end{gathered}`

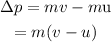
Substituting the known values,

`\begin{gathered} \Delta p=0.14(-37-28.8) \\ \Delta p=-0.14*65.8 \\ \Delta p=-9.212\text{ kgm/s} \end{gathered}`

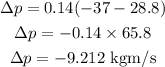
Thus, the time at which the bat and ball were in contact is,

`\begin{gathered} F=(|\Delta p|)/(\Delta t) \\ \Delta t=(|\Delta p|)/(F) \end{gathered}`

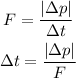
Substituting the known values,

`\begin{gathered} \Delta t=(9.212)/(5000) \\ \Delta t=0.0018\text{ s} \\ \Delta t=1.8*10^(-3)\text{ s} \end{gathered}`

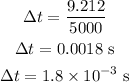
Thus, the ball and bat were in contact for 0.0018 seconds.