Question

Which system of equations can you use to find the roots of the equation? 1) x³-10x = x²-6 2) y = x³ -x² + 10x + 6 3) y = x³ -x² + 10x 4) y = x² -6

Answer 1

The system of equations that can be used to find the roots of the given equation is
`\(y = x³ - x² + 10x + 6\).`

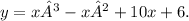
Step-by-step explanation:

The equation provided is
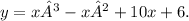`\(y = x³ - x² + 10x + 6\).`To find its roots, we need a system of equations where the left side is set equal to zero. Therefore, the correct system is
`\(x³ - x² + 10x + 6 = 0\).`

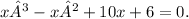
Now, let's break down the equation. It is a cubic equation with terms involving
`\(x³\), \(x²\), \(x\)`, and a constant. To find the roots, we set
`\(y\) (or \(f(x)\))` equal to zero and solve for
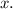`\(x\).` The roots of the cubic equation correspond to the values of
`\(x\)` where the equation equals zero.

In this case, the system
`\(x³ - x² + 10x + 6 = 0\)` represents the cubic equation
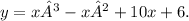`\(y = x³ - x² + 10x + 6\).` By solving this system, you can determine the values of x that make the given cubic equation equal to zero, thus finding its roots.

It's important to note that the other provided equations do not match the given equation, so they do not represent the correct system for finding its roots. The correct system is the one where the equation is set to zero, allowing for the determination of the values of x that satisfy the given cubic equation.