Question

The dashed triangle is a dilation image of the solid triangle with the center at the origin. Is the dilation an enlargement or a reduction? Find the scale factor of the dilation.

Answer 1

If the scale factor
`\(k\)` in the dilation of the dashed triangle from the solid triangle with the center at the origin is greater than 1, it is an enlargement; if
`\(0 < k < 1\)`, it is a reduction. Calculate
`\(k\)` using the formula
`\(k = \sqrt{((kx_2 - kx_1)^2 + (ky_2 - ky_1)^2)/((x_2 - x_1)^2 + (y_2 - y_1)^2)}\) for any pair of corresponding vertices.`

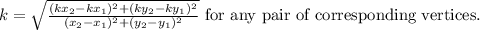
Step-by-step explanation:

To determine whether the dilation is an enlargement or a reduction, we need to examine the relative sizes of corresponding sides of the dashed and solid triangles.

Let's denote the vertices of the solid triangle as
`\(A(x_1, y_1)\), \(B(x_2, y_2)\)`, and
`\(C(x_3, y_3)\)`, and the corresponding vertices of the dashed triangle after dilation as
`\(A'(kx_1, ky_1)\), \(B'(kx_2, ky_2)\)`, and
`\(C'(kx_3, ky_3)\)`, where
`\(k\)` is the scale factor.

The distance between two points
`\((x_1, y_1)\)` and
`\((x_2, y_2)\)` can be calculated using the distance formula:

`\[ d = √((x_2 - x_1)^2 + (y_2 - y_1)^2) \]`

Now, let's consider the sides of the triangles. The ratio of corresponding side lengths in the dilation is given by:

`\[ \text{Scale Factor (k)} = \frac{\text{Length of corresponding side in dashed triangle}}{\text{Length of corresponding side in solid triangle}} \]`

If
`\(k > 1\)`, it means the length of corresponding sides in the dashed triangle is greater than the length of corresponding sides in the solid triangle, indicating an enlargement. If
`\(0 < k < 1\)`, it means the length of corresponding sides in the dashed triangle is less than the length of corresponding sides in the solid triangle, indicating a reduction.

Let's calculate the scale factor using the distance formula for each pair of corresponding vertices. If the scale factor is greater than 1, it's an enlargement; if it's between 0 and 1, it's a reduction.

`\[ k = (d(A', B'))/(d(A, B)) = (√((kx_2 - kx_1)^2 + (ky_2 - ky_1)^2))/(√((x_2 - x_1)^2 + (y_2 - y_1)^2)) \]`

Similarly, calculate
`\(k\)` for the other two pairs of corresponding vertices
`\(C\)` and
`\(A\)`, as well as
`\(B\)` and
`\(C\)`. The overall
`\(k\)` should be the same for all pairs. This
`\(k\)` is the scale factor of the dilation.