Final Answer:
The angles that are also equal to 60° are 2) 7 and 4) 6.
Explanation
In trigonometry, angles are often denoted as θ (theta), and in this case, we are given the angle
 . To find angles equal to 60°, we look for angles with the same measure.
. To find angles equal to 60°, we look for angles with the same measure.
Let's start by examining each option:
1. Angle 3: No information is provided about this angle's measure.
2. Angle 7: This angle is opposite to
 , forming a vertically opposite pair. By the Vertical Angles Theorem,
, forming a vertically opposite pair. By the Vertical Angles Theorem,
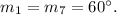
3. Angle 8: There is no information about the measure of this angle.
4. Angle 6: This angle is adjacent to
 forming a linear pair. By the Linear Pair Postulate, the sum of the measures of
forming a linear pair. By the Linear Pair Postulate, the sum of the measures of
 and
and
 Therefore,
Therefore,
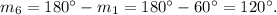
5. Angle 2: No information is provided about this angle's measure.
6. Angle 5: No information is provided about this angle's measure.
Based on these calculations and geometric principles:
- Angle 7
 is equal to the given angle
is equal to the given angle
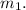
- Angle 6
 is not equal to
is not equal to
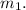
Therefore, the correct angles equal to 60° are 2) 7 and 4) 6. This conclusion is reached by applying the Vertical Angles Theorem and the Linear Pair Postulate, demonstrating a thorough understanding of geometric principles.