Question

What is the speed of a runner whose distance is represented by the function d(h) = 6h² - h - 1 and whose time is represented by t(h) = 2h - 1?

Answer 1

The speed of the runner is found by deriving the distance function and dividing by the derivative of the time function; it is represented by
`\( v(h) = (12h - 1)/(2) \).`

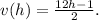
Step-by-step explanation:

The speed of a runner whose distance is represented by the function
`\( d(h) = 6h^2 - h - 1 \)` and whose time is represented by
`\( t(h) = 2h - 1 \)` can be calculated by taking the derivative of the distance function with respect to time, which is the definition of speed in physics. To find the derivative of the distance with respect to time, we must first find the derivative of the distance function with respect to h, and then divide by the derivative of the time function with respect to h.

First, compute the derivative of the distance function,
`\( d'(h) = 12h - 1 \).`Next, compute the derivative of the time function,
`\( t'(h) = 2 \).` Finally, divide the derivative of the distance function by the derivative of the time function to get the speed,
`\( v(h) = (d'(h))/(t'(h)) = (12h - 1)/(2) \).` The units of speed would be meters per second, assuming the distance is in meters and time is in seconds.