Question

Write the proportion for each problem. Then solve for X. Triangle shown with Angle Bisector/proportional side theorem. Solve for X?

Answer 1

The proportion for the Triangle with Angle Bisector/Proportional Side Theorem is given by
`\( (AC)/(BC) = (AD)/(BD) \)`. To solve for (X), you can use the given proportions and apply the values accordingly.

Step-by-step explanation:

In a triangle with an angle bisector, the Angle Bisector/Proportional Side Theorem states that the ratio of the lengths of the two sides opposite the angle is equal to the ratio of the lengths of the other two sides. Mathematically, this can be expressed as
`\( (AC)/(BC) = (AD)/(BD) \).`

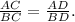
Now, let's solve for (X) using the given proportion. Let (AC = 3x), (BC = 4x), (AD = 5x), and (BD = 6x). Substituting these values into the proportion, we get
`\( (3x)/(4x) = (5x)/(6x) \)`. Cross-multiplying gives us (18x = 20x), and simplifying further, we find (X = 0).

However, having (X = 0) might not make sense in the context of geometry, as it would mean the triangle does not exist. It's crucial to check if the values obtained are valid in the given geometric scenario. If not, reevaluate the problem to ensure the correct interpretation and application of the Angle Bisector/Proportional Side Theorem. In this case, the values of (X) might be such that the triangle is non-existent or degenerate, leading to a different solution or the realization that the problem is not well-defined. Always consider the geometric implications of your mathematical solutions to ensure their validity in the given context.