Question

Given: Line a and line b intersect. Prove: 1 2 3. Statements: 1. Line a and line b intersect. 1. Given. 2. _____ 3. 3 is supplementary tO₂. Reasons: 2. _____ 3. Linear pair theorem. Which statement and reason best completes the proof? 1) 2. Definition of supplementary angles. 2. Linear pair theorem. 2) A. m 1 + m $4 = 180° 3) B. 2. $2 is supplementary to $4 4) C. 2m 2 + m *3 = 180° 5) D. 2. $1 is supplementary to $2

Answer 1

The statement and reason that best complete the proof are Option C:"2. 2m₂ + m₃ = 180°" and Reason: "Linear pair theorem."

Step-by-step explanation:

The given proof involves demonstrating the relationship between angles formed by the intersection of Line
`\(a\)` and Line
`\(b\)`. Let
`\(m_2\)` and
`\(m_3\)` represent the measures of the angles formed. The linear pair theorem states that supplementary angles add up to \(180°\). Therefore, the calculation for Option C is as follows:

`\[2m_2 + m_3 = 2 * \text{measure of angle } m_2 + \text{measure of angle } m_3\]`

This expression corresponds to the sum of the measures of angles formed by Line
`\(a\)` and Line
`\(b\)`. According to the linear pair theorem, when these angles are supplementary, their sum equals
`\(180\)`. Thus, Option C accurately represents the relationship between the angle measures and is the appropriate choice for completing the proof.

Option A, suggesting
`\(m_1 + m_4 = 180\)` based on the definition of supplementary angles, is not applicable to this context. The given statements involve angles
`\(m_2\)` and
`\(m_3\)`, not
`\(m_1\)` and
`\(m_4\)`. Options B and D do not directly address the measures of the angles involved in the proof.

By selecting Option C and citing the linear pair theorem as the reason, the proof logically establishes the supplementary relationship between the angles formed by the intersection of Line
`\(a\)` and Line
`\(b\).`

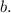
So correcct option is Option C