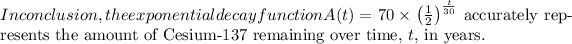Question

A radioactive substance, Cesium-137, has a half-life of about 30 years. This means that, after every 30 years, half of the amount of Cesium-137 present turns into something else. If the initial amount of Cesium-137 was 70 grams, which exponential decay function represents the amount of Cesium-137 remaining over time, t, in years?

Answer 1

The exponential decay function representing the amount of Cesium-137 remaining over time, \( t \), in years is given by:

`\[ A(t) = A_0 * \left((1)/(2)\right)^{(t)/(T)} \]`

where:

- A(t) is the amount of Cesium-137 remaining at time t,

- A_0 is the initial amount of Cesium-137,

- T is the half-life of Cesium-137.

Step-by-step explanation:

The exponential decay formula describes the decay of a substance over time. In this case, the formula is
`\( A(t) = A_0 * \left((1)/(2)\right)^{(t)/(T)} \), where \( A(t) \) is the amount of Cesium-137 at time \( t \), \( A_0 \) is the initial amount, and \( T \) is the half-life.`

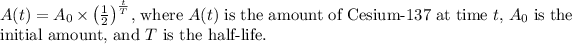
For Cesium-137, with a half-life of 30 years, the formula becomes
`\( A(t) = 70 * \left((1)/(2)\right)^{(t)/(30)} \)`, where 70 is the initial amount.

This formula represents the exponential decay of Cesium-137 over time. As t increases in multiples of 30, the exponent term reduces by 1, indicating the halving of the amount. The initial 70 grams will be halved after 30 years, halved again after 60 years, and so on.

`In conclusion, the exponential decay function \( A(t) = 70 * \left((1)/(2)\right)^{(t)/(30)} \) accurately represents the amount of Cesium-137 remaining over time, \( t \), in years.`