Question

The diagram shows six triangles, each having sides of 3cm, 7cm, and 8cm. What is the perimeter of this 12-sided shape?

Answer 1

The perimeter of the 12-sided shape formed by the six triangles, each having sides of 3cm, 7cm, and 8cm, is
`\(12 * 8\,\text{cm} = 96\,\text{cm}\).`

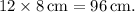
Explanation:

The diagram depicts six identical triangles, each with side lengths of 3cm, 7cm, and 8cm. The triangles form a regular dodecagon, a 12-sided polygon, with each side of the dodecagon being equal to the perimeter of one of these triangles.

To find the perimeter of the entire shape, we multiply the length of one side by the total number of sides (12). Therefore, the perimeter \(P\) is calculated as
`\(P = 12 * 8\,\text{cm} = 96\,\text{cm}\).`

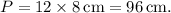
The sides of the triangles are in the ratio 3:7:8, which corresponds to a Pythagorean triple, indicating that the triangles are right-angled triangles. The most common Pythagorean triple is the 3-4-5 triangle, and by scaling it up, we obtain the 3-7-8 triangle.

The right angles in each triangle ensure that when the triangles are arranged in a regular dodecagon, the angles at the vertices sum up to form a complete circle. The perimeter of the dodecagon is, therefore, the sum of the lengths of its 12 equal sides.

In conclusion, the perimeter of the 12-sided shape is 96cm. This solution highlights the application of basic geometric principles and the Pythagorean triple relationship in determining the perimeter of regular polygons formed by identical triangles.