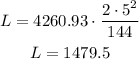We have the following, L, of the beam varies as the product of the width and the square of the height:
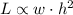
And varies inversely as the lenght of the wooden beam:
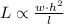
therefore:
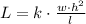
where k is the proportionality constant
w = 4, h=8, l = 216 and L = 5050
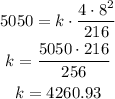
now, if w = 2, h = 5, l = 144: