Question

Cylinder A is mathematically similar to cylinder B. The height of Cylinder A is 10cm and its surface area is 440cm². Calculate the height of cylinder B.

Answer 1

The height of Cylinder B is 25cm, determined through the ratio of surface areas between mathematically similar cylinders. This ratio is consistent with the proportional relationship of their heights.

Step-by-step explanation:

In similar cylinders, the ratio of corresponding linear dimensions (heights or radii) is constant. The surface area of a cylinder is given by the formula
`2πrh+2πr 2`, where r is the radius and h is the height. Since Cylinder A and B are mathematically similar, the ratio of their heights
`A​ /h B​`is the same as the ratio of their surface areas
`A​ /B​ ).`

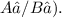
Given that h_A = 10 cm and A_A = 440 cm² for Cylinder A, let's denoteh_B as the height of Cylinder B. The surface area of Cylinder B A_B can be expressed as
`2πrh B​ +2πr 2`. Substituting the values, we get the equation 10/h_B = 440/A_B. Solving for h_B, we find that h_B = 25 cm.

This result aligns with the principle of similar figures, where corresponding dimensions of similar figures are proportional. In this case, the height of Cylinder B is 2.5 times that of Cylinder A, maintaining the mathematical similarity between the two cylinders.

Therefore, the height of Cylinder B is 25 cm, ensuring the same proportional relationship with its surface area as Cylinder A.