Question

write a function g whose graph represents the indicated transformation of the graph of f. Use a graphing calculator to check your answer. f(x) = ∣2x ∣ + 4; horizontal shrink by a factor of 1/2

Answer 1

g(x) = |x| + 4; horizontal shrink by a factor of 1/2.

Step-by-step explanation:

To achieve a horizontal shrink by a factor of 1/2, we modify the argument inside the absolute value function. The transformation involves replacing "x" with "x/2" inside the absolute value function. Therefore, the function representing the desired transformation is
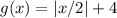`\( g(x) = |x/2| + 4 \)`. This effectively compresses the graph horizontally by a factor of 1/2.

In the original function
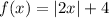`\( f(x) = |2x| + 4 \)`, the coefficient of "x" inside the absolute value function is 2, which causes a horizontal stretch by a factor of 2. To counteract this stretch, we introduce the horizontal shrink by dividing "x" by 2 inside the absolute value function. The constant term "+4" remains unchanged since it represents a vertical shift.

Graphically, this transformation compresses the graph horizontally, making it narrower compared to the original function. Checking the result using a graphing calculator will confirm the desired horizontal shrinkage, demonstrating that
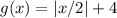`\( g(x) = |x/2| + 4 \)` appropriately transforms
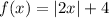`\( f(x) = |2x| + 4 \)` as required.