Question

Tomework Solve the exponential equa e^(-c)=4^(2c)

Answer 1

The value of c in the exponential equation
`e^(-c)` =
`4^(2c) is c` =
`-ln(2) / (2 * ln(2) + 1).`

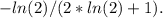
Step-by-step explanation:

To solve the equation
`e^(-c)` =
`4^(2c)`, we'll start by expressing
`4^(2c)`in terms of e, as e is the base of the natural logarithm and makes calculations easier.

Recall that 4 can be written as
`e^(2` ln(2)) since 4 is the same as
`(e^(ln(2)))^2`. Therefore,
`4^(2c)` can be rewritten as
`(e^(2` ln
`(2)))^(2c)`, which simplifies to
`e^(4c` ln
`(2))`.

So, now the equation
`e^(-c)` =
`e^(4c` ln
`(2))` can be expressed as
`e^(-c) = e^(4c` ln(2)). To solve this equation, we can equate the exponents:
`-c = 4c` ln
`(2)`.

Solving for c, we get
`-c = 4c` ln
`(2)`. Rearranging terms gives us
`-c = 4`ln(2)c. Dividing both sides by -c, we get
`1 = -4ln(2)`.

Finally, solving for c, we find
`c = -ln(2) / (4ln(2))` =
`-ln(2) / (2` ln
`(2) + 1)`. Therefore, this is the value of c that satisfies the exponential equation
`e^(-c) = 4^(2c)`.