Question

Gaph of the given function on the given interval (b) x=y \3/2 −50≤y≤44

Answer 1

The graph of the function
`\(x = y^(3/2) - 50\)` on the interval
`\(-50 \leq y \leq 44\)` forms a curve. The relationship between
`\(x\)` and
`\(y\)` is characterized by the expression
`\(x = y^(3/2) - 50\).`

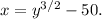
Step-by-step explanation:

To visualize the graph of the given function,
`\(x = y^(3/2) - 50\)`, on the specified interval
`\(-50 \leq y \leq 44\),` we can evaluate the function for various values of
`\(y\)` within this range. The function is defined as the cube root of
`\(y\)` raised to the power of 2, minus 50. As
`\(y\)` changes,
`\(x\)` will also change accordingly, producing a curve on the coordinate plane.

Calculating and plotting points by substituting different values of
`\(y\)` within the given interval will illustrate the shape of the curve. The interval
`\(-50 \leq y \leq 44\)` ensures that we explore the function within a specific range, which contributes to understanding the behavior of the curve over that interval.

In summary, the graph of the function
`\(x = y^(3/2) - 50\)` on the interval
`\(-50 \leq y \leq 44\)` will reveal a curve. The equation's structure, involving the cube root of
`\(y\)` raised to the power of 2, influences the curve's shape, and examining the function within the specified interval provides a focused view of its behavior.