Question

Let { x−a ∣x 2 −a 2 ∣ ​ , (x+a) 2 ​ if x

Answer 1

The expression is equal to (x + a)^2 if x ≠ a, and undefined when x = a.

Step-by-step explanation:

The given expression is a piecewise function, defined as follows:

`\[ f(x) =\begin{cases} (x - a) & \text{if } x \\eq a \\(x + a)^2 & \text{if } x = a \end{cases}\]`

For
`\( x \\eq a \),` the expression
`\( x^2 - a^2 \)` can be factored as ( (x - a)(x + a) ). Therefore,
`\( ((x - a))/((x - a)) * |x^2 - a^2| \)`simplifies to ( |x + a| ). This results in the first part of the piecewise function:
`\( (x - a) \) for \( x \\eq a \).`

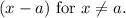
For ( x = a ), substituting ( a ) into
`\( |x^2 - a^2| \)` yields
`\( |a^2 - a^2| \),` which is 0. Thus,
`\( ((x + a)^2)/(|x^2 - a^2|) \)`becomes
`\( ((a + a)^2)/(0) \)`, leading to an undefined value.

In summary, the given expression simplifies to ( (x - a) ) for
`\( x \\eq a \)` and is undefined for ( x = a ). This piecewise definition ensures a smooth transition between the two cases and accurately represents the behavior of the expression for all values of ( x ).