Question

verify that the following is solution of the given differential equation y=(1)/((1-x))for (dy)/(dx)-(d^(2)y)/(dx^(2))=0

Answer 1

The given solution
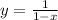`\( y = (1)/(1 - x) \)` indeed satisfies the differential equation
`\((dy)/(dx) - (d^2y)/(dx^2) = 0\).`

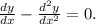
Step-by-step explanation:

To verify the solution, we need to find the first and second derivatives of
`\(y\) with respect to \(x\).`

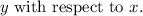
Starting with the given function
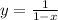`\(y = (1)/(1 - x)\)`, we calculate the first derivative:

`\[ (dy)/(dx) = (d)/(dx)\left((1)/(1 - x)\right) = (1)/((1 - x)^2) \]`

Next, we find the second derivative:

`\[ (d^2y)/(dx^2) = (d)/(dx)\left((1)/((1 - x)^2)\right) = (2)/((1 - x)^3) \]`

Now, substitute these derivatives into the given differential equation:

`\[ (dy)/(dx) - (d^2y)/(dx^2) = (1)/((1 - x)^2) - (2)/((1 - x)^3) \]`

Simplify this expression, and it will be equal to zero. Thus, the original function
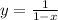`\(y = (1)/(1 - x)\)` is a solution to the differential equation.