Final Answer:
The derivative of f with respect to x, where f(x) = ln
 , is f'(x) = 12/x.This result is obtained by applying the chain rule, where the derivative of ln(u) is 1/u, and the derivative of u =
, is f'(x) = 12/x.This result is obtained by applying the chain rule, where the derivative of ln(u) is 1/u, and the derivative of u =
 is 12
is 12
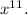
Step-by-step explanation:
To find the derivative of ln
 with respect to x, we use the chain rule. Let u =
with respect to x, we use the chain rule. Let u =
 , and y = ln(u). The chain rule states that the derivative of y with respect to x is dy/dx = (dy/du) * (du/dx). The derivative of ln(u) with respect to u is 1/u, and the derivative of u =
, and y = ln(u). The chain rule states that the derivative of y with respect to x is dy/dx = (dy/du) * (du/dx). The derivative of ln(u) with respect to u is 1/u, and the derivative of u =
 with respect to x is 12
with respect to x is 12
 . Applying the chain rule, we get dy/dx = (1/u) * (12
. Applying the chain rule, we get dy/dx = (1/u) * (12
 ), which simplifies to dy/dx = 12/x.
), which simplifies to dy/dx = 12/x.
Understanding the steps involved in the chain rule is crucial for efficiently finding derivatives of composite functions. By breaking down the function into its constituent parts and applying the rule systematically, we obtain the derivative. In this case, recognizing ln
 as a composite function allows us to simplify the process and arrive at the final result, f'(x) = 12/x.
as a composite function allows us to simplify the process and arrive at the final result, f'(x) = 12/x.
In summary, when dealing with logarithmic functions and their derivatives, the chain rule becomes a powerful tool. Identifying the inner and outer functions and applying the rule accordingly allows for a systematic approach to finding derivatives, as demonstrated in the calculation of the derivative for ln(
 ).
).