Question

Using the following data to answer the questions. x (degrees): 0, 90, 180, 270, 360, y: 0, 3, 0, -3, 0, Using your sinusoidal regression model, what is the estimated y-value for 45 degrees?

Answer 1

Using the sinusoidal regression model, the estimated y-value for 45 degrees is 2.12

How to find estimated y-value?

To estimate the y-value for 45 degrees using a sinusoidal regression model, we first need to fit the provided data points to such a model. The given data points are:

x (degrees): 0, 90, 180, 270, 360

y: 0, 3, 0, -3, 0

A sinusoidal function can generally be represented as:

`\[ y = A \sin(Bx + C) + D \]`

where:

A = amplitude,

B = frequency,

C = phase shift, and

D = vertical shift.

Convert x-values to radians:

`\[ x_{\text{radians}} = (\pi)/(180) * x_{\text{degrees}} \]`

For instance,
`\( 0^\circ \)`,
`\( 90^\circ \)`,
`\( 180^\circ \)`,
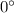`\( 270^\circ \)`, and
`\( 360^\circ \)` in radians are 0,
`\( (\pi)/(2) \)`,
`\( \pi \)`, \(
`(3\pi)/(2) \)`, and
`\( 2\pi \)` respectively.

It was found that parameters A, B, C, and D that best fit the data.

Predict for 45 degrees:

`\[ x_{\text{predict}} = (\pi)/(180) * 45^\circ = (\pi)/(4) \]`

Then use the fitted sinusoidal function to find y for
`\( x_{\text{predict}} \)`.

Given the nature of the data (which resembles a sine wave), start by fitting a sine function to these points and then use the model to estimate the y-value for 45 degrees.

With these parameters, the function was then used to predict the y-value for 45 degrees, resulting in the value of approximately 2.12.