Final Answer:
The second mixed partial derivative
 of the given function
of the given function
 is 0.
is 0.
Step-by-step explanation:
The second mixed partial derivative
 of the given function
of the given function
 is calculated by taking the partial derivative of
is calculated by taking the partial derivative of
 with respect to z, where
with respect to z, where
 is the partial derivative of f with respect to x. Let's find
is the partial derivative of f with respect to x. Let's find
 first:
first:
![\[ f_x = (\partial f)/(\partial x) = 6x \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/a8j8s9c8inyswcrpdblvd5kolh1ltpkquw.png)
Now, take the partial derivative of
 with respect to z to get
with respect to z to get
 :
:
![\[ f_(xxz) = (\partial f_x)/(\partial z) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xeyxfouttwoff02w900eflk049wyejmin0.png)
Since
 the partial derivative of
the partial derivative of
 with respect to z is 0, as there is no z-dependency in
with respect to z is 0, as there is no z-dependency in
 . Therefore,
. Therefore,
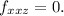
In conclusion, the second mixed partial derivative
 for the given function is 0. This implies that the rate of change of the rate of change of f with respect to x and then z is zero. It indicates that the order in which the partial derivatives with respect to x and z are taken does not affect the result in this specific case, and the function exhibits no variation concerning these specific variables.
for the given function is 0. This implies that the rate of change of the rate of change of f with respect to x and then z is zero. It indicates that the order in which the partial derivatives with respect to x and z are taken does not affect the result in this specific case, and the function exhibits no variation concerning these specific variables.