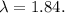Final Answer:
a. The estimated mean
 of the Poisson distribution, based on the sample data, is calculated to be
of the Poisson distribution, based on the sample data, is calculated to be
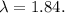
b. The hypotheses are:
![\[ H_0: \text{The number of power failures follows a Poisson distribution with } \lambda = 1.84 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wo1w872p8kotkrvc0jnu4gwmxfrdb8agbz.png)
![\[ H_1: \text{The number of power failures does not follow a Poisson distribution with } \lambda = 1.84 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9tkml1a9kdabt8ap7viw21wal6hvpnw8fh.png)
c. The expected frequencies for each category are calculated using the Poisson distribution formula, and these values are placed in the last row of the table. If any expected frequency is less than 5, the corresponding cells are combined.
d. The test statistic
 is calculated using the sample data and the expected frequencies.
is calculated using the sample data and the expected frequencies.
e. The critical value of the test
 is determined.
is determined.
f. Comparing the calculated test statistic to the critical value, if
 , we reject
, we reject
 . In this case, we would conclude that the number of power failures per day does not follow a Poisson distribution with
. In this case, we would conclude that the number of power failures per day does not follow a Poisson distribution with
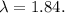
Step-by-step explanation:
a. The estimated mean of the Poisson distribution
 is calculated from the sample data using the formula
is calculated from the sample data using the formula
 where
where
 is the frequency and
is the frequency and
 is the number of power failures in each category.
is the number of power failures in each category.
b. The null hypothesis
 assumes that the observed data follows a Poisson distribution with
assumes that the observed data follows a Poisson distribution with
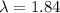 , while the alternative hypothesis
, while the alternative hypothesis
 suggests otherwise.
suggests otherwise.
c. Expected frequencies are calculated using the Poisson distribution formula:
 . These values are then placed in the last row of the table. If any expected frequency is less than 5, the corresponding cells are combined to meet the assumption of the chi-square test.
. These values are then placed in the last row of the table. If any expected frequency is less than 5, the corresponding cells are combined to meet the assumption of the chi-square test.
d. The test statistic
 is calculated using the formula:
is calculated using the formula:
 , where
, where
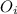 is the observed frequency and
is the observed frequency and
 is the expected frequency.
is the expected frequency.
e. The critical value
 is determined based on the degrees of freedom and the significance level.
is determined based on the degrees of freedom and the significance level.
f. By comparing the calculated test statistic to the critical value, a decision is made on whether to reject the null hypothesis. If
 we reject
we reject
 , indicating that the number of power failures per day does not follow a Poisson distribution with
, indicating that the number of power failures per day does not follow a Poisson distribution with