Final Answer:
The probability density function (pdf) of Y is given by:
![\[ f_Y(y) = (1)/(4)e^{-(y^2)/(2)}, \quad y \in \mathbb{R} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/raz1k7zro0san2zu7vg927ctll8qxwvt9n.png)
Step-by-step explanation:
The transfer characteristic of the nonlinear amplifier relates the input \(X\) to the output \(Y\) through a piecewise function. When
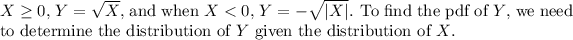
First, consider the case when
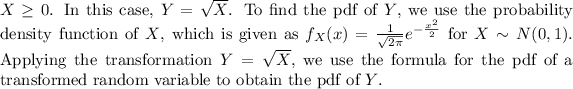
Next, when
