Question

(Continuing previous PP.) In the meeting time problem, assume that Regina's R and Cady's Y arrival times in (0,1) each follow a Uniform (0,1) distribution, independently of each other. Note: in previous versions of this problem time was measured in minutes after noon, but here we are measuring time in hours after noon, e.g. 0.25 corresponds to 12:15. Let W=∣R−Y∣ be the amount of time (hours) the first person to arrive waits for the second person to arrive. It can be shown that W has pdf f W ​ (w)=2(1−w),0

Answer 1

The pdf of the waiting time W, denoted as
`f_W(w)`, is given by
`f_W(w) = 2(1-w)` within the range of
`0 < = W < = 1`. The pdf represents the probability density at each point w, with the density decreasing as w increases.

Step-by-step explanation:

The problem describes the arrival times of two individuals, Regina (R) and Cady (Y), using a Uniform (0,1) distribution. We want to find the probability density function (pdf) of the waiting time (W) for the first person to wait for the second person to arrive.

Given that the pdf of W is
`f_W(w) = 2(1-w)`, we can break down the problem into steps:

1. Understand the probability density function (pdf):

• - The pdf,
  `f_W(w)`, represents the probability density at each point w.
• - In this case, the pdf
  `f_W(w) = 2(1-w)` means that the density at any point w is equal to
  `2(1-w)`.

2. Determine the range of possible values for W:

• - The waiting time (W) can take any value between 0 and 1, as both R and Y have arrival times between 0 and 1.
• - Therefore, the range of possible values for W is
  `0 < = W < = 1`.

3. Calculate the probability density function (pdf) within the given range:

• - Since the pdf
  `f_W(w) = 2(1-w)`, we can substitute w with any value within the range of 0 to 1.
• - For example, if we substitute w = 0.5, we get
  `f_W(0.5) = 2(1-0.5) = 2(0.5) = 1.`
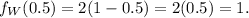
• - This means that at
  `w = 0.5`, the density is equal to 1.

4. Visualize the pdf
`f_W(w)`:

• - The graph of
  `f_W(w) = 2(1-w)` will be a straight line with a slope of -2, starting from (0,2) and ending at (1,0).
• - The graph will be below the x-axis, indicating that the probability density decreases as w increases.