Question

2. Let f(x)= x 2 −25 10 ​ . a. Find f ′ (x) and determine the critical numbers of f.

Answer 1

To find the critical numbers of the function f(x) = (x^2 - 25)/10, we first calculate its derivative, which is f'(x) = x/5. Setting this equal to zero gives us a single critical number, x = 0. There are no critical numbers where the derivative is undefined as it is defined for all real numbers.

Step-by-step explanation:

The question asks us to find the derivative of the function f(x) =
`(x^2 - 25)/(10)` and determine its critical numbers. The derivative of a function gives us the slope at any point along the curve of the function, and critical numbers are the values of x at which the derivative is zero or undefined, indicating potential maxima, minima, or points of inflection.

To find the derivative of f(x), we use the power rule. The derivative of x^n is n*x^(n-1), so the derivative of x^2 is 2*x. Since we are dividing by 10, and derivative is a linear operator, the derivative of the entire function is:

`f'(x) = (2*x)/(10) = (x)/(5)`

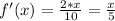
To find the critical numbers, we set the derivative equal to zero:

`0 = (x)/(5)`

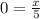
Thus, x = 0 is the only critical number for this function. Since the derivative is defined for all real numbers, there are no critical numbers due to the derivative being undefined.