Question

Suppose that \( X \) is either 1 or 2. If \( E[X]=1.6 \), find \( \operatorname{Pr}[X=1] \).

Answer 1

X is either 1 or 2. If
`\( E[X]=1.6 \)` then the probability that X is equal to 1 is
`\( (2)/(5) \)`.

Step-by-step explanation:

Expected value E[X] is the sum of all possible values of X multiplied by their respective probabilities. In this case, we have:

E[X] = 1 . Pr[X=1] + 2 . Pr[X=2]

Since E[X] = 1.6, we can write the equation as

1 . Pr[X=1] + 2 . Pr[X=2] = 1.6.

We also know that the sum of the probabilities of all possible outcomes is:

1(Pr[X=1] +Pr[X=2] = 1).

Solving these two equations simultaneously, we find:

Pr[X=1] =
`(2)/(5) \).`

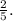
In probability theory, the expected value is a measure of the "center" of the distribution, and finding the probabilities of individual outcomes helps us characterize the distribution fully. In this case, knowing E[X] allows us to set up equations that relate the probabilities of X=1 and X=2, and solving these equations gives us the specific probabilities. Therefore, the probability of X being equal to 1 is
`\( (2)/(5) \)`.

In conclusion, by understanding the relationship between expected value and individual probabilities, we can determine the likelihood of specific outcomes in a probability distribution.