Question

Find the derivative of the function. g(w)=9 3 w ​

Answer 1

The derivative of the function
`\(g(w) = (9)/(3w)\) is \(g'(w) = -3w^(-2)\).`

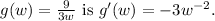
Step-by-step explanation:

To find the derivative of the given function
`\(g(w) = (9)/(3w)\)` , we can apply the power rule of differentiation. The power rule states that if
`\(f(x) = ax^n\),` then
`\(f'(x) = nax^((n-1))\).` In this case,
`\(g(w) = (9)/(3w)\)` can be rewritten as
`\(g(w) = 3w^(-1)\).` Applying the power rule, the derivative
`\(g'(w)\) is then \(-3w^(-2)\).`

Understanding differentiation rules is fundamental in calculus, as it allows us to find the rate at which a function changes. In this case, the negative exponent in the derivative indicates that as
`\(w\)` increases, the function
`\(g(w)\)` decreases at a rate proportional to the square of
`\(w\)`. This information is valuable in analyzing the behavior of functions and their slopes.

Derivatives have widespread applications, from physics and engineering to economics. They provide insights into the instantaneous rate of change of a quantity with respect to another, and mastering the rules of differentiation enables a deeper understanding of the dynamic nature of mathematical functions.