Question

Assume the random variable X is normaly distributed with mean μ=50 and standard deviation α=7 Compute the probabiity. Be sure to draw a normal curve with the area corresponding to the probability shaded. P(34

Answer 1

The probability
`\( P(34 < X < \infty) \)`, where
`\( X \)` is a normally distributed random variable with mean
`\( \mu = 50 \)` and standard deviation
`\( \alpha = 7 \),` can be calculated using the standard normal distribution. By converting the values to z-scores, the probability can be found. The shaded area under the normal curve corresponds to the probability of
`\( P(34 < X < \infty) \).`

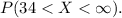
Step-by-step explanation:

To calculate the probability
`\( P(34 < X < \infty) \)` for a normally distributed random variable
`\( X \)` with mean
`\( \mu = 50 \)` and standard deviation
`\( \alpha = 7 \),` we need to standardize the values using z-scores. The z-score formula is
`\( Z = \frac{{X - \mu}}{{\alpha}} \).` For the lower bound
`\( X = 34 \)`, the corresponding z-score is
`\( Z = \frac{{34 - 50}}{{7}} = -2.29 \).` To find the probability, we consult a standard normal distribution table or calculator, which yields the area to the left of
`\( Z = -2.29 \)`. Since we are interested in the probability
`\( P(34 < X < \infty) \)`, we are looking for the complement of the area to the left of
`\( Z = -2.29 \)`, which is the area to the right.

The normal distribution curve represents the probability density function, and the shaded area to the right of
`\( Z = -2.29 \)` corresponds to the probability
`\( P(34 < X < \infty) \)`. This probability indicates the likelihood that a randomly selected value from the distribution is greater than 34. The standard normal distribution is a useful tool for such calculations, allowing us to determine probabilities for different ranges of values in a normal distribution.

In summary, the probability
`\( P(34 < X < \infty) \)` is found by standardizing the lower bound, finding the corresponding z-score, and then determining the complement of the area to the left of this z-score on the standard normal distribution curve. This process provides a quantitative measure of the likelihood of values greater than 34 in the given normal distribution.