Final Answer:
The invariant measure for the Markov chain on
 with transition probability
with transition probability
 for all
for all
 is
is
 for all i , where c is a constant.
for all i , where c is a constant.
Step-by-step explanation:
In a Markov chain, an invariant measure is a probability measure that remains unchanged by the transition probabilities. For the given Markov chain on
 , with the transition probability
, with the transition probability
 , the chain only moves to the right, indicating that the probability mass is shifted to the right at each step. This implies that the probability distribution does not depend on the specific position i leading to a constant invariant measure.
, the chain only moves to the right, indicating that the probability mass is shifted to the right at each step. This implies that the probability distribution does not depend on the specific position i leading to a constant invariant measure.
Mathematically, for an invariant measure
 , we require
, we require
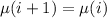 for all i . Since
for all i . Since
 the transition probability from i to i+1 is certain. Therefore,
the transition probability from i to i+1 is certain. Therefore,
 ensuring that the probability mass remains constant as the chain progresses.
ensuring that the probability mass remains constant as the chain progresses.
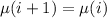
The constant
 represents the invariant measure, and its value can be determined by normalization, ensuring that the probabilities sum up to 1.
represents the invariant measure, and its value can be determined by normalization, ensuring that the probabilities sum up to 1.