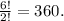Final Answer:
a.
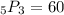
b.
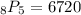
c.
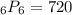
d.

e.
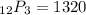
f.
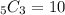
g.
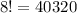
h.
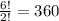
Step-by-step explanation:
a.
 represents the permutation of 3 elements chosen from a set of 5. The formula for permutations is
represents the permutation of 3 elements chosen from a set of 5. The formula for permutations is
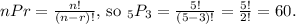
b.
 is the permutation of 5 elements chosen from a set of 8, calculated using the permutation formula.
is the permutation of 5 elements chosen from a set of 8, calculated using the permutation formula.
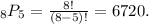
c.
 is the permutation of all 6 elements in a set of 6, giving
is the permutation of all 6 elements in a set of 6, giving
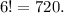
d.
 is the factorial of 2 multiplied by the factorial of 3, which equals 12.
is the factorial of 2 multiplied by the factorial of 3, which equals 12.
e.
 represents the permutation of 3 elements chosen from a set of 12. Calculated using the permutation formula,
represents the permutation of 3 elements chosen from a set of 12. Calculated using the permutation formula,
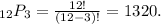
f.
 is the combination of 3 elements chosen from a set of 5. The combination formula is
is the combination of 3 elements chosen from a set of 5. The combination formula is
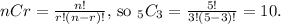
g.
 is the factorial of 8, which is
is the factorial of 8, which is
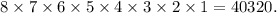
h.
 is the factorial of 6 divided by the factorial of 2, giving
is the factorial of 6 divided by the factorial of 2, giving