Question

The weight of a new born calf of a particular breed of cattle in normally distributed with a mean =90lbs and a standard deviation of 12lbs. You select a random sample of 9 weights from a data in a Farmers Journal. According to the Central Limit Theorem, what is the resulting mean and standard deviation of the sampling distribution of samples of n=9 from the population? Mean =90 and Std. Dev. =12 Mean =90 and Std. Dev. =4 Mean =90 and Std. Dev. =3 Mean =30 and Std. Dev, =4

Answer 1

The resulting mean and standard deviation of the sampling distribution of samples of ( n=9 ) from the population, according to the Central Limit Theorem, are
`\( \text{Mean} = 90 \) and \( \text{Std. Dev.} = (12)/(√(9)) = 4 \).`

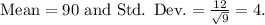
Step-by-step explanation:

According to the Central Limit Theorem (CLT), when random samples are drawn from a population, regardless of the shape of the population distribution, the sampling distribution of the sample means will be approximately normally distributed if the sample size is sufficiently large. In this case, the given population has a mean
`(\( \mu \))` of 90 lbs and a standard deviation
`(\( \sigma \))` of 12 lbs. The CLT states that the mean of the sampling distribution of sample means
`(\( \bar{X} \))` is equal to the population mean (\( \mu \)), and the standard deviation of
`\( \bar{X} \) is equal to \( (\sigma)/(√(n)) \), where \( n \) is the sample size`.

For this problem, since ( n = 9 ), the standard deviation of the sampling distribution is
`\( (12)/(√(9)) = 4 \) lbs.` Therefore, the resulting mean and standard deviation of the sampling distribution are
`\( \text{Mean} = 90 \) and \( \text{Std. Dev.} = 4 \) lbs`, respectively.

This means that when we take random samples of size ( n = 9 ) from the population of newborn calf weights, the distribution of the sample means will have a mean of 90 lbs and a standard deviation of 4 lbs, illustrating the Central Limit Theorem in action.