Question

suppose that X1, X2,...,Xn are independent random variable, each with the uniform distribution on [c-d,c+d] where c is unknow and d is known (-[infinity] < c < [infinity] , d > 0). Find the maximum likelih

Answer 1

The maximum likelihood estimate (MLE) for the unknown parameter
`\(c\)` in the given scenario is the midpoint of the range [c-d, c+d], denoted as
`\(\hat{c} = (X_((1)) + X_((n)))/(2)\),`where
`\(X_((1))\)` is the minimum observed value and
`\(X_((n))\)` is the maximum observed value.

Step-by-step explanation:

In statistics, the likelihood function represents the probability of the observed data given a certain parameter. For a uniform distribution on [c-d, c+d], the probability density function (pdf) is constant within this interval. The joint probability density function for n independent and identically distributed random variables is the product of their individual pdfs. In this case, the likelihood function is
`\(L(c) = \prod_(i=1)^(n) (1)/(2d)\).`

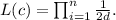
To find the MLE for
`\(c\)`, we maximize the likelihood function. This is equivalent to maximizing the logarithm of the likelihood function, which simplifies calculations. Taking the logarithm allows us to convert the product in the likelihood function to a sum. The log-likelihood function is then differentiated with respect to
`\(c\)`, and the critical points are found by setting the derivative equal to zero. Solving for
`\(c\)` results in the MLE expression
`\(\hat{c} = (X_((1)) + X_((n)))/(2)\)`, where
`\(X_((1))\)` and
`\(X_((n))\)` are the minimum and maximum observed values, respectively.

In conclusion, the MLE for
`\(c\)` in a uniform distribution on [c-d, c+d] is the midpoint of the observed range, which is
`\(\hat{c} = (X_((1)) + X_((n)))/(2)\)`. This estimator maximizes the likelihood of the observed data under the given distribution.