Final Answer:
The contingency table for the given information is as follows:
```
| HIV Positive | HIV Negative | Total
-----------------|--------------|--------------|-------
Elisa Positive | 0.259 * P | 0.001 * P | 0.26P
Elisa Negative | 0.074 * P | 0.666 * P | 0.74P
-----------------|--------------|--------------|-------
Total | 0.333 * P | 0.667 * P | P
```
Explanation:
To construct the contingency table, we first decide on a hypothetical total population size denoted as
 . The lower right box represents the total population size. Given the prevalence of HIV as 25.9%, we calculate the lower left box, which is the total number of individuals with HIV, as
. The lower right box represents the total population size. Given the prevalence of HIV as 25.9%, we calculate the lower left box, which is the total number of individuals with HIV, as
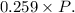
The total number of individuals without HIV is then obtained by subtracting the HIV-positive individuals from the total population, resulting in
 . With these totals, we use the conditional probabilities provided to fill in the other boxes.
. With these totals, we use the conditional probabilities provided to fill in the other boxes.
The Elisa Positive and HIV Positive cell is filled with
 representing the probability of testing positive given that an individual has HIV.
representing the probability of testing positive given that an individual has HIV.
Similarly, the Elisa Positive and HIV Negative cell is filled with
 ,
,
 representing the probability of testing positive given that an individual does not hav
representing the probability of testing positive given that an individual does not hav
 e HIV. The Elisa Negative and HIV Positive cell is filled with
e HIV. The Elisa Negative and HIV Positive cell is filled with
 and the Elisa Negative and HIV Negative cell is filled with
and the Elisa Negative and HIV Negative cell is filled with

In summary, the contingency table is constructed by utilizing the prevalence, conditional probabilities, and the chosen hypothetical total population size. This table serves as a valuable tool for understanding the relationship between HIV status and Elisa test results in a given population.