Question

Micaela and Danielle each improved their yards by planting daylilies and shrubs. They bought their supplies from the same store. Micaela spent $74 on 12 daylilies and 10 shrubs. Danielle spent $39 on 7 daylilies and 5 shrubs. Find the cost of one daylily and the cost of one shrub.

Answer 1

Given:

Let the cost of each daylily be d

Let the cost of each shrub be s

Generating the system of equations;

`\begin{gathered} 12d+10s=74.................(1) \\ 7d+5s=39.....................(2) \end{gathered}`

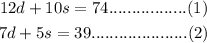
Equation (2) multiplied by 2;

`\begin{gathered} 12d+10s=74..............(1) \\ 14d+10s=78...............(2) \\ \\ Subtracting\text{ equation \lparen1\rparen from equation \lparen2\rparen; equation \lparen2\rparen- equation \lparen1\rparen} \\ 14d-12d=78-74 \\ 2d=4 \\ Dividing\text{ both sides by 2;} \\ d=(4)/(2) \\ d=2 \end{gathered}`

Substituting the value of d into equation (2);

`\begin{gathered} 7d+5s=39 \\ 7(2)+5s=39 \\ 14+5s=39 \\ 5s=39-14 \\ 5s=25 \\ Dividing\text{ both sides by 5;} \\ s=(25)/(5) \\ s=5 \end{gathered}`

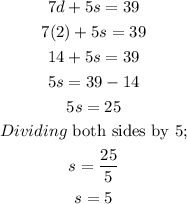
Therefore, the cost of one daylily is $2 and the cost of one shrub is $5.