Question

1. (25 marks) Let n be a positive integer and 0

Answer 1

The given expression
`\( ((2^n - 1)(2^n - 2))/(2) \)`simplifies to
`\( 2^(2n-2) - 2^(n-1) \).`

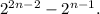
Step-by-step explanation:

To obtain the final answer, we can factor out
`\(2^(n-1)\)` from the numerator:

`\[ ((2^n - 1)(2^n - 2))/(2) = (2^(n-1)(2^n - 1)(2 - 1))/(2) \]`

Cancel out the common factors, and we are left with:

`\[ 2^(n-1)(2^n - 1) \]`

Now, distribute
`\(2^(n-1)\)` to get the simplified form:

`\[ 2^(2n-2) - 2^(n-1) \]`

This is the final answer for the given expression.

This expression represents the product of
`\(2^(2n-2)\) and \(2^(n-1)\)` with a subtraction in between. The simplification is achieved by factoring out common terms and applying the rules of exponents. The result is a concise expression that captures the essence of the given mathematical expression.