Question

Can someone help me with this question? In a survey, 15 people were asked how much they spent on their child's last birthday gift. The results were roughly bell-shaped with a mean of \( \$ 33 \) and standard deviation of \$8. Construct a co

Answer 1

The confidence interval for the average amount spent on a child's last birthday gift, based on the survey data, is approximately \( \(\$33 \pm \$3.06\) at a 95% confidence level.

Step-by-step explanation:

In constructing a confidence interval for the mean, we can use the formula:

`\[ \text{Confidence Interval} = \text{Mean} \pm (\text{Critical Value} * \text{Standard Error}) \]`

The critical value for a 95% confidence interval with 14 degrees of freedom (15 respondents - 1) is approximately 2.145 (obtained from a t-table). The standard error (\(SE\)) is calculated as
`\( \frac{\text{Standard Deviation}}{\sqrt{\text{Sample Size}}} \).`

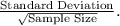
Given the mean
`(\( \bar{X} = \$33 \))`, standard deviation
`(\(SD = \$8\))`, and sample size (\(n = 15\)), we find
`\(SE = (\$8)/(√(15)) \approx \$2.06\)`. Plugging in these values into the formula:

`\[ \text{Confidence Interval} = \$33 \pm (2.145 * \$2.06) \]`

This yields the interval
`\( \$33 \pm \$3.06\)`.

Therefore, we can be 95% confident that the average amount spent on a child's last birthday gift falls within the range of approximately \$29.94 to \$36.06.

This confidence interval provides a useful estimate of the likely range for the population mean based on the sample data, helping us make informed conclusions about the average spending on birthday gifts for children in the larger population.