Question

At a large university, the probability that a student takes calculus is 0.06. If a student is on the dean's list, the probability that they take calculus is 0.08. The probability that a student is on the dean's list is 0.2. a. Find the probability that a student takes calculus AND is on the dean's list. b. Find the probability that a student takes calculus OR is on the dean's list. c. Are the events "taking Calculus" and "being on the dean's list" mutually exlusive? Explain d. Are the events "taking Calculus" and "being on the dean's list" independent? Explain

Answer 1

a. The probability that a student takes calculus AND is on the dean's list is 0.016.

b. The probability that a student takes calculus OR is on the dean's list is 0.244.

c. The events "taking Calculus" and "being on the dean's list" are not mutually exclusive.

d. The events "taking Calculus" and "being on the dean's list" are not independent.

Step-by-step explanation:

In part a, we find the probability of the intersection of the events "taking calculus" and "being on the dean's list" by multiplying the probability of being on the dean's list (0.2) by the conditional probability of taking calculus given that a student is on the dean's list (0.08). Therefore,
`\(0.2 * 0.08 = 0.016\).`

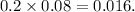
In part b, we calculate the probability of the union of the two events using the formula
`\(P(A \cup B) = P(A) + P(B) - P(A \cap B)\).` Substituting the given probabilities, we get
`\(0.06 + 0.2 - 0.016 = 0.244\).`

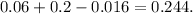
In part c, events are mutually exclusive if they cannot occur at the same time. Since the probability of both being on the dean's list and taking calculus is not zero (0.016), these events are not mutually exclusive.

In part d, two events are independent if the occurrence of one does not affect the occurrence of the other. In this case, since the probability of taking calculus changes when a student is on the dean's list (0.08), the events are not independent.