Question

Graph the solution to the following system of inequalities.ys-2x-3y> 4x + 710-8-4-Х?10

Answer 1

Step-by-step explanation

`\begin{gathered} y\leq-2x-3 \\ y>4x+7 \end{gathered}`

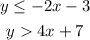
Step 1

First, graph the inequality 1

`y\leq-2x-3`

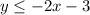
the related equation is

`y=-2x-3`

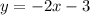
now, get 2 coordinates of the line

a) when x=1

`\begin{gathered} y=-2x-3 \\ y=-2(1)-3 \\ y=-2-3 \\ y=-5 \\ so,\text{ the coordinate is (1,-5)} \end{gathered}`

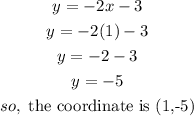
b)when x=0

`\begin{gathered} y=-2x-3 \\ y=-2\cdot0-3 \\ y=0-3 \\ y=-3 \\ \text{coordinate P2}\Rightarrow(0,-3) \end{gathered}`

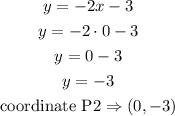
now, draw a line that pases trought the coordinates we found.

Since the inequality is ≤ , not a strict one, the border line is solid

Step 2

Now, do the same for inequality 2

so

`y>4x+7`

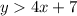
the related equation is

`y=4x+7`

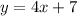
find 2 coordinates of the line

a)when x=0

`\begin{gathered} y=4x+7 \\ y=4\cdot0+7 \\ y=0+7 \\ y=7 \\ so,\text{ the coordinate 3 is (0,7)} \end{gathered}`

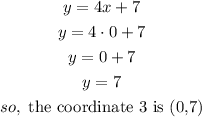
b) when x=-2

`\begin{gathered} y=4x+7 \\ y=4\cdot-2+7 \\ y=-8+7 \\ y=-1 \\ so,\text{ the coordinate 4 is (-2},-1) \end{gathered}`

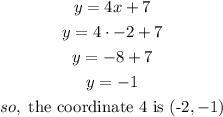
now, draw the line 2, this lines passes trougth the coordiantes 3 and 4

Since the inequality is >, a strict one, the border line is dotted

Step 3

Graph:

in inequality (1) we need the values smaller r than -2x-3, it measn all values under the line,

and in Inequality 2 we need the values greater than 4x+7, it means all values over the line

so, the solution is the dark purple zone

I hope this helps you