Step-by-step explanation
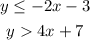
Step 1
First, graph the inequality 1
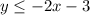
the related equation is
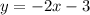
now, get 2 coordinates of the line
a) when x=1
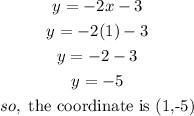
b)when x=0
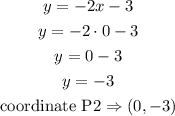
now, draw a line that pases trought the coordinates we found.
Since the inequality is ≤ , not a strict one, the border line is solid
Step 2
Now, do the same for inequality 2
so
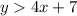
the related equation is
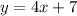
find 2 coordinates of the line
a)when x=0
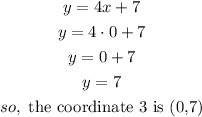
b) when x=-2
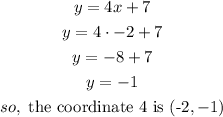
now, draw the line 2, this lines passes trougth the coordiantes 3 and 4
Since the inequality is >, a strict one, the border line is dotted
Step 3
Graph:
in inequality (1) we need the values smaller r than -2x-3, it measn all values under the line,
and in Inequality 2 we need the values greater than 4x+7, it means all values over the line
so, the solution is the dark purple zone
I hope this helps you