Question

light, with a wavelength of 604 nm traveling through air encounters a pane of glass with an index of refraction of 1.45. what is the frequency of the light inside of the glass, in hz?

Answer 1

The frequency of the light inside of the glass, given that the refractive index of the glass is 1.45, is
`3.43*10^(14)\ Hz`

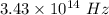
How to calculate the frequency of the light inside the glass?

First, we shall obtain the speed of the inside the glass. This is shown below:

• Refractive index of glass (n) = 1.45
• Speed of light in vacuum (c) = 3×10⁸ m/s
• Speed of light in glass (v) =?

`v = (c)/(n) \\\\v = (3*10^8)/(1.45)\\\\v = 2.07*10^8\ m/s`

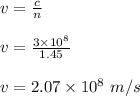
Finally, we shall obtain the frequency of the light inside the glass. This shown below:

• Wavelength of light (λ) = 604 nm = 604 × 1×10⁻⁹ m
• Velocity of light (v) = 2.07×10⁸ m/s
• Frequency of light inside glass (f) =?

`f = (v)/(\lambda) \\\\f = (2.07*10^8)/(604*10^(-9)) \\\\f = 3.43*10^(14)\ Hz`