Question

hint 1 hint 2 a 32-g ball at the end of a string is swung in a vertical circle with a radius of 35 cm. the tangential velocity is 200.0 cm/s. find the tension in the string:

Answer 1

The tension in the string is approximately 3.658 N.

To solve this problem

The acceleration that is directed toward the circle's center is known as the centripetal acceleration and is calculated as follows:

`a_c = v^2/r`

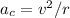
Where

v stands for the tangential speed.

The circle's radius is denoted by r.

Plugging in the given values, we get:

`a_c = (200.0 cm/s)^2 / (35 cm) = 114.29 cm/s^2`

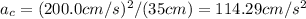
Now, let calculate the tension in the string

The mass of the ball multiplied by the centripetal acceleration equals the tension in the string, which represents the net force acting on the ball.

`T = m * a_c`

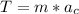
Where

T is the tension in the string

m is the mass of the ball

Plugging in the given values, we get:

T =
`(0.032 kg) * (114.29 cm/s^2)` = 3.658 N

Therefore, the tension in the string is approximately 3.658 N.