Question

suppose that a department contains 10 men and 20 women. how many different committees of 6 members are possible if the committee must have strictly more women than men? your answer is:

Answer 1

If the committee must have strictly more women than men, the possible number of committees is 373,065 committees

How to find the possible committees

To find the number of different committees of 6 members with strictly more women than men, we can consider the possible scenarios based on the number of men and women in the committee.

The total number of committee members is fixed at 6.

Scenario 1: 5 women and 1 man

Choose 5 women from the 20 available women:
`\(\binom{20}{5}\)` = 15504

Choose 1 man from the 10 available men:
`\(\binom{10}{1}\)` = 10

Scenario 2: 4 women and 2 men

Choose 4 women from the 20 available women:
`\(\binom{20}{4}\)` = 4845

Choose 2 men from the 10 available men:
`\(\binom{10}{2}\)` = 45

Now, sum up the possibilities for the two scenarios:

`\binom{20}{5} * \binom{10}{1} + \binom{20}{4} * \binom{10}{2}`

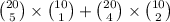
= 15504 * 10 + 4845 * 45

= 373,065