Question

Solve and classify the given system of linear equations. a) p = 4q-2 b) 4q-p-2=0

Answer 1

The solution to the given system of linear equations is q = -1 and p = -6.

Step-by-step explanation:

The system of linear equations is given by:

a)
`\( p = 4q - 2 \)`

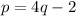
b)
`\( 4q - p - 2 = 0 \)`

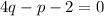
To find the solution, we can substitute the expression for p from equation (a) into equation (b):

`\[ 4q - (4q - 2) - 2 = 0 \]`

Simplifying the equation:

`\[ 4q - 4q + 2 - 2 = 0 \]`

[ 0 = 0 ]

This equation is satisfied for any value of q, indicating that q can be any real number. Now, substitute the value of q back into equation (a) to find p:

`\[ p = 4(-1) - 2 = -6 \]`

Therefore, the solution to the system of linear equations is q = -1 and p = -6.

In summary, the system is consistent and has a unique solution. The values q = -1 and p = -6 satisfy both equations, making them the solution to the given system. This implies that the two equations represent two lines that intersect at the point (q, p) = (-1, -6) in the coordinate plane.