Question

the first term of an arithmetic sequence is 2, and the common diffrence is 9. Find two consecutives terms of the sequence that have a sum of 355. What positions in the sequence are the terms?

Answer 1

The consecutive terms of the arithmetic sequence with a first term of 2 and a common difference of 9 that have a sum of 355 are the terms at positions n = 18 and n = 19. The terms are \
`(a_(18) = 161\) and \(a_(19) = 170\).`

Step-by-step explanation:

In an arithmetic sequence, each term is obtained by adding a fixed difference to the previous term. The general form of an arithmetic sequence is given by
`a_n`=
`a_1` + (n-1 )d, where \
`(a_n\) is the \(n\)-th term, \(a_1\)`is the first term, \(n\) is the position in the sequence, and \(d\) is the common difference.

In this case, the first term
`(\(a_1\))` is 2, and the common difference dis 9. Therefore, the n-th term of the sequence is given by
`\(a_n = 2 + 9(n-1)\).`

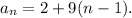
We are looking for two consecutive terms whose sum is 355. Let's represent these terms as
`a_n` and
`\(a_(n+1)\)`. The sum of these terms is given by
`\(a_n + a_(n+1) = 355\).`

Substituting the expression for \(a_n\) into the equation, we get
`\(2 + 9(n-1) + 2 + 9n = 355\).`

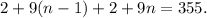
Solving this equation, we find n = 18. Therefore, the terms at positions n = 18 and n = 19 have a sum of 355. Substituting n = 18 into the expression for
`\(a_n\)`, we find
`\(a_(18) = 161\)`, and for n = 19, we find
`\(a_(19) = 170\).` So, the consecutive terms at positions 18 and 19 in the sequence have a sum of 355.