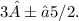Final Answer:
The correct solution to the quadratic equation
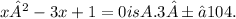
Step-by-step explanation:
The quadratic formula is given by
 where a, b, and c are the coefficients of the quadratic equation ax² + bx + c = 0. In this case, the equation is
where a, b, and c are the coefficients of the quadratic equation ax² + bx + c = 0. In this case, the equation is
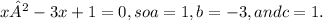
Now, substituting these values into the quadratic formula:
![\[ x = (-(-3) \pm √((-3)^2 - 4(1)(1)))/(2(1)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bixpl7573mw1a8f88ed02qiql05xl4nwms.png)
Simplifying further:
![\[ x = (3 \pm √(9 - 4))/(2) \]\[ x = (3 \pm √(5))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/dhuewhppo2jp5ixhougd1g1ck1uhlst2lb.png)
This gives us two solutions:
![\[ x_1 = (3 + √(5))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4ayjt14y1ndv49hfrqhnqg4iyhca9cq7hl.png)
![\[ x_2 = (3 - √(5))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1ejr3rrwcs6vyyfl27ord59s8dsnbfcp35.png)
These solutions can be further simplified by multiplying the numerator and denominator of each fraction by the conjugate of the denominator:
![\[ x_1 = (3 + √(5))/(2) \cdot (√(5) + 1)/(√(5) + 1) = (3√(5) + 3 + 5 + √(5))/(2(√(5) + 1)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4igaqhz0zjmlaizwxr19r98myqglfp8sxa.png)
![\[ x_2 = (3 - √(5))/(2) \cdot (√(5) - 1)/(√(5) - 1) = (3√(5) - 3 + 5 - √(5))/(2(√(5) - 1)) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/54pkyt60hsiksljgl5hs42tdlksarjbhwk.png)
Simplifying both expressions, we get:
![\[ x_1 = (3 + √(5))/(2) = 3 + (√(5))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8ejisz2aji67q5mp4jb826pdurbgsugqqf.png)
![\[ x_2 = (3 - √(5))/(2) = 3 - (√(5))/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/swjh838s1irhkq7sz6tl7ga5mpwjjjf9h4.png)
Thus, the solutions are
 which can be expressed as
which can be expressed as